1. 導入庫
import numpy as np #矩陣運算
import matplotlib.pyplot as plt #可視化
import random #產(chǎn)生數(shù)據(jù)擾動
2. 產(chǎn)生數(shù)據(jù)
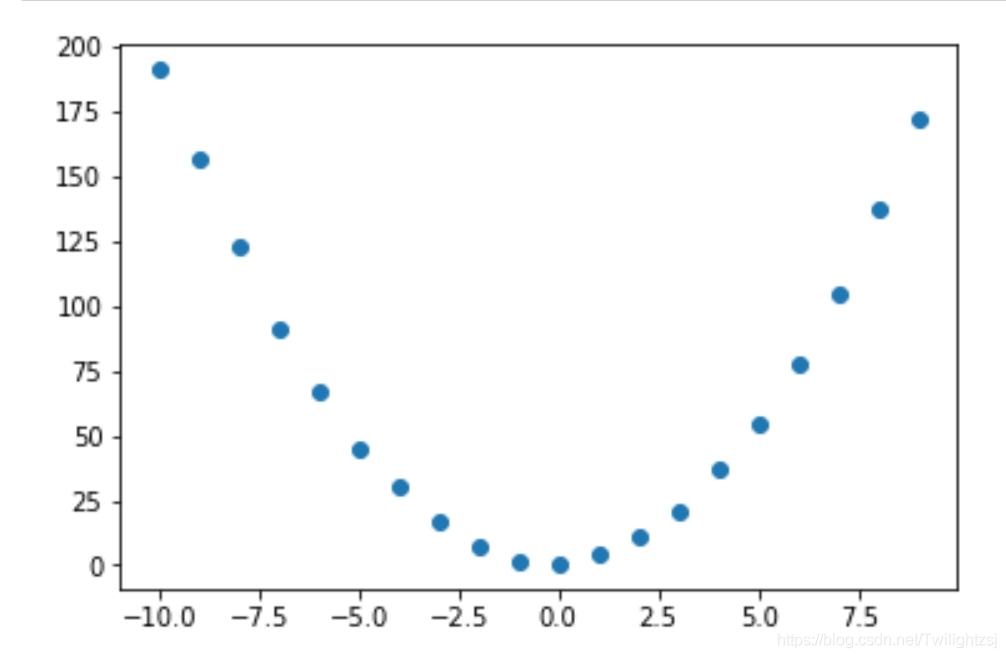
擬合曲線 y = 2 × x2 + x + 1
X_m = np.mat([[i**2, i, 1] for i in range(-10,10)]) #矩陣類型,用于運算
y_m = np.mat([[2*x[0,0]+x[0,1]+1+random.normalvariate(0,1)] for x in X_m]) #矩陣類型�����,用于運算
X_a = np.asarray(X_m[:,1].T)[0] #array類型��,用于可視化
y_a = np.asarray(y_m.T)[0] #array類型��,用于可視化
plt.scatter(X_a, y_a) #顯示數(shù)據(jù)
plt.show()
3. BGD
def BGD(X,y,w0,step,e): #批量梯度下降法
n=0
while n=10000:
w1 = w0-step*X.T.dot(X.dot(w0)-y)/X.shape[0]
dw = w1-w0;
if dw.dot(dw.T)[0,0] = e**2:
return w1
n += 1
w0 = w1
return w1
4. 計算
w_m = BGD(X_m,y_m,np.mat([[5],[3],[2]]),1e-4,1e-20) #可自行調(diào)參
w_a = np.asarray(w_m.T)[0]
print(w_a)
array([1.99458492, 0.91587829, 1.48498921])
5. 評價( R 2)
y_mean = y_a.mean()
y_pre = np.array([w_a[0]*x[0,0]+w_a[1]*x[0,1]+w_a[2] for x in X_m])
SSR = ((y_pre-y_mean)**2).sum()
SST = ((y_a-y_mean)**2).sum()
R2 = SSR/SST
print(R2)
0.9845542903194531
我們可以認為擬合效果不錯��。如果 R 2 R^{2} R2的值接近0�����,可能需要重新調(diào)參��。
6. 結(jié)果展示
X = np.linspace(-10,10,50)
y = np.array([w_a[0]*x**2+w_a[1]*x+w_a[2] for x in X])
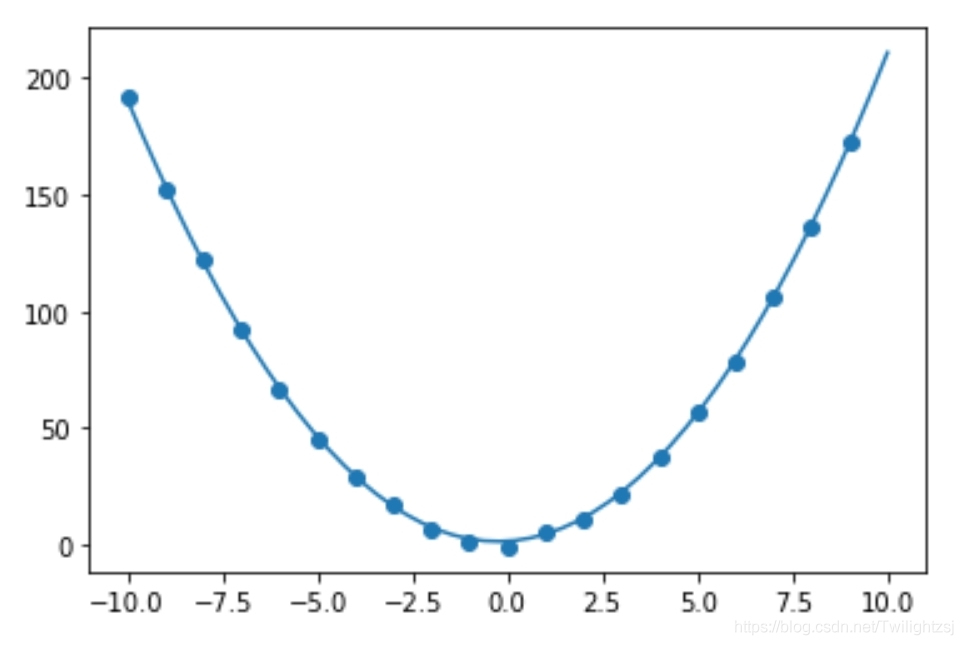
plt.scatter(X_a,y_a)
plt.plot(X,y)
plt.show()
到此這篇關(guān)于Python實現(xiàn)批量梯度下降法(BGD)擬合曲線的文章就介紹到這了,更多相關(guān)Python 批量梯度下降內(nèi)容請搜索腳本之家以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持腳本之家����!
您可能感興趣的文章:- python應用Axes3D繪圖(批量梯度下降算法)
- Python編程實現(xiàn)線性回歸和批量梯度下降法代碼實例