了解知道Dropout原理
如果要提高神經(jīng)網(wǎng)絡(luò)的表達或分類能力，最直接的方法就是采用更深的網(wǎng)絡(luò)和更多的神經(jīng)元，復雜的網(wǎng)絡(luò)也意味著更加容易過擬合。
于是就有了Dropout，大部分實驗表明其具有一定的防止過擬合的能力。
用代碼實現(xiàn)Dropout
Dropout的numpy實現(xiàn)
PyTorch中實現(xiàn)dropout
import torch.nn.functional as F
import torch.nn.init as init
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
import numpy as np
import math
%matplotlib inline
#%matplotlib inline 可以在Ipython編譯器里直接使用
#功能是可以內(nèi)嵌繪圖，并且可以省略掉plt.show()這一步。
xy=np.loadtxt('./data/diabetes.csv.gz',delimiter=',',dtype=np.float32)
x_data=torch.from_numpy(xy[:,0:-1])#取除了最后一列的數(shù)據(jù)
y_data=torch.from_numpy(xy[:,[-1]])#取最后一列的數(shù)據(jù)，[-1]加中括號是為了keepdim
print(x_data.size(),y_data.size())
#print(x_data.shape,y_data.shape)
#建立網(wǎng)絡(luò)模型
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
self.l1=torch.nn.Linear(8,60)
self.l2=torch.nn.Linear(60,4)
self.l3=torch.nn.Linear(4,1)
self.sigmoid=torch.nn.Sigmoid()
self.dropout=torch.nn.Dropout(p=0.5)
def forward(self,x):
out1=self.sigmoid(self.l1(x))
out2=self.dropout(out1)
out3=self.sigmoid(self.l2(out2))
out4=self.dropout(out3)
y_pred=self.sigmoid(self.l3(out4))
return y_pred
#our model
model=Model()
criterion=torch.nn.BCELoss(size_average=True)
#optimizer=torch.optim.SGD(model.parameters(),lr=0.1)
optimizer=torch.optim.Adam(model.parameters(),lr=0.1,weight_decay=0.1)
#weight_decay是L2正則
#training loop
Loss=[]
for epoch in range(2000):
y_pred=model(x_data)
loss=criterion(y_pred,y_data)
if epoch%20 == 0:
print("epoch = ",epoch," loss = ",loss.data)
optimizer.zero_grad()
loss.backward()
optimizer.step()
hour_var = Variable(torch.randn(1,8))
print("predict",model(hour_var).data[0]>0.5)
L2正則化
optimizer=torch.optim.SGD(model.parameters(),lr=0.01,weight_decay=0.001)
補充：PyTorch1.0實現(xiàn)L1，L2正則化以及Dropout (附dropout原理的python實現(xiàn)以及改進)
看代碼吧~
# 包
import torch
import torch.nn as nn
import torch.nn.functional as F
# torchvision 包收錄了若干重要的公開數(shù)據(jù)集、網(wǎng)絡(luò)模型和計算機視覺中的常用圖像變換
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
1. 什么是dropout（隨機失活）？
1.1 一種Regularization的方法
與L1、L2正則化和最大范式約束等方法互為補充。在訓練的時候，dropout的實現(xiàn)方法是讓神經(jīng)元以超參數(shù) p 的概率被激活或者被設(shè)置為0。
1.2 在訓練過程中
隨機失活可以被認為是對完整的神經(jīng)網(wǎng)絡(luò)抽樣出一些子集，每次基于輸入數(shù)據(jù)只更新子網(wǎng)絡(luò)的參數(shù)（然而，數(shù)量巨大的子網(wǎng)絡(luò)們并不是相互獨立的，因為它們都共享參數(shù)）。
1.3 在測試過程中不使用隨機失活
所有的神經(jīng)元都激活，**但是對于隱層的輸出都要乘以 p **。可以理解為是對數(shù)量巨大的子網(wǎng)絡(luò)們做了模型集成（model ensemble），以此來計算出一個平均的預(yù)測。詳見：http://cs231n.github.io/neural-networks-2/
1.4 一般在全連接層把神經(jīng)元置為0
在卷積層中可能把某個通道置為0!
2. 用代碼實現(xiàn)regularization(L1、L2、Dropout）
注意：PyTorch中的regularization是在optimizer中實現(xiàn)的，所以無論怎么改變weight_decay的大小，loss會跟之前沒有加正則項的大小差不多。這是因為loss_fun損失函數(shù)沒有把權(quán)重W的損失加上！
2.1 L1 regularization
對于每個 ω 我們都向目標函數(shù)增加一個λ|ω| 。
L1正則化有一個有趣的性質(zhì)，它會讓權(quán)重向量在最優(yōu)化的過程中變得稀疏（即非常接近0）。也就是說，使用L1正則化的神經(jīng)元最后使用的是它們最重要的輸入數(shù)據(jù)的稀疏子集，同時對于噪音輸入則幾乎是不變的了。
相較L1正則化，L2正則化中的權(quán)重向量大多是分散的小數(shù)字。在實踐中，如果不是特別關(guān)注某些明確的特征選擇，一般說來L2正則化都會比L1正則化效果好。
PyTorch里的optimizer只能實現(xiàn)L2正則化，L1正則化只能手動實現(xiàn)：
regularization_loss = 0
for param in model.parameters():
regularization_loss += torch.sum(abs(param))
calssify_loss = criterion(pred,target)
loss = classify_loss + lamda * regularization_loss
optimizer.zero_grad()
loss.backward()
optimizer.step()
2.2 L2 regularization
對于網(wǎng)絡(luò)中的每個權(quán)重 ω ，向目標函數(shù)中增加一個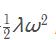 
其中 λ 是正則化強度。這樣該式子關(guān)于梯度就是 λω 了。
L2正則化可以直觀理解為它對于大數(shù)值的權(quán)重向量進行嚴厲懲罰，傾向于更加分散的權(quán)重向量。
最后需要注意在梯度下降和參數(shù)更新的時候，使用L2正則化意味著所有的權(quán)重都以 w += -lambda * W向著0線性下降。
選擇一個合適的權(quán)重衰減系數(shù)λ非常重要，這個需要根據(jù)具體的情況去嘗試，初步嘗試可以使用 1e-4 或者 1e-3
在PyTorch中某些optimizer優(yōu)化器的參數(shù)weight_decay (float, optional)就是 L2 正則項，它的默認值為0。
optimizer = torch.optim.SGD(model.parameters(),lr=0.01,weight_decay=0.001)
2.3 PyTorch1.0 實現(xiàn) dropout
數(shù)據(jù)少, 才能凸顯過擬合問題, 所以我們就做10個數(shù)據(jù)點.
torch.manual_seed(1) # Sets the seed for generating random numbers.reproducible
N_SAMPLES = 20
N_HIDDEN = 300
# training data
x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
print('x.size()',x.size())
# torch.normal(mean, std, out=None) → Tensor
y = x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))
# test data
test_x = torch.unsqueeze(torch.linspace(-1, 1, N_SAMPLES), 1)
test_y = test_x + 0.3*torch.normal(torch.zeros(N_SAMPLES, 1), torch.ones(N_SAMPLES, 1))
# show data
plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.5, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.5, label='test')
plt.legend(loc='upper left')
plt.ylim((-2.5, 2.5))
plt.show()
x.size() torch.Size([20, 1])
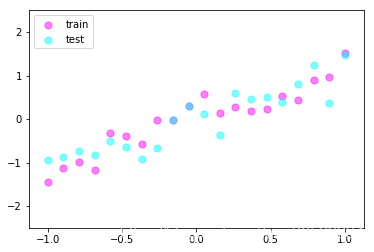
我們現(xiàn)在搭建兩個神經(jīng)網(wǎng)絡(luò), 一個沒有 dropout, 一個有 dropout. 沒有 dropout 的容易出現(xiàn) 過擬合, 那我們就命名為 net_overfitting, 另一個就是 net_dropped.
net_overfitting = torch.nn.Sequential(
torch.nn.Linear(1,N_HIDDEN),
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN,N_HIDDEN),
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN,1),
)
net_dropped = torch.nn.Sequential(
torch.nn.Linear(1,N_HIDDEN),
torch.nn.Dropout(0.5), # 0.5的概率失活
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN,N_HIDDEN),
torch.nn.Dropout(0.5),
torch.nn.ReLU(),
torch.nn.Linear(N_HIDDEN,1),
)
訓練模型并測試2個模型的performance
optimizer_ofit = torch.optim.Adam(net_overfitting.parameters(),lr=0.001)
optimizer_drop = torch.optim.Adam(net_dropped.parameters(),lr=0.01)
loss = torch.nn.MSELoss()
for epoch in range(500):
pred_ofit= net_overfitting(x)
pred_drop= net_dropped(x)
loss_ofit = loss(pred_ofit,y)
loss_drop = loss(pred_drop,y)
optimizer_ofit.zero_grad()
optimizer_drop.zero_grad()
loss_ofit.backward()
loss_drop.backward()
optimizer_ofit.step()
optimizer_drop.step()
if epoch%50 ==0 :
net_overfitting.eval() # 將神經(jīng)網(wǎng)絡(luò)轉(zhuǎn)換成測試形式,此時不會對神經(jīng)網(wǎng)絡(luò)dropout
net_dropped.eval() # 此時不會對神經(jīng)網(wǎng)絡(luò)dropout
test_pred_ofit = net_overfitting(test_x)
test_pred_drop = net_dropped(test_x)
# show data
plt.scatter(x.data.numpy(), y.data.numpy(), c='magenta', s=50, alpha=0.5, label='train')
plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='cyan', s=50, alpha=0.5, label='test')
plt.plot(test_x.data.numpy(), test_pred_ofit.data.numpy(), 'r-', lw=3, label='overfitting')
plt.plot(test_x.data.numpy(), test_pred_drop.data.numpy(), 'b--', lw=3, label='dropout(50%)')
plt.text(0, -1.2, 'overfitting loss=%.4f' % loss(test_pred_ofit, test_y).data.numpy(), fontdict={'size': 20, 'color': 'red'})
plt.text(0, -1.5, 'dropout loss=%.4f' % loss(test_pred_drop, test_y).data.numpy(), fontdict={'size': 20, 'color': 'blue'})
plt.legend(loc='upper left')
plt.ylim((-2.5, 2.5))
plt.pause(0.1)
net_overfitting.train()
net_dropped.train()
plt.ioff()
plt.show()
一共10張圖片就不一一放上來了，取1,4,7,10張吧：
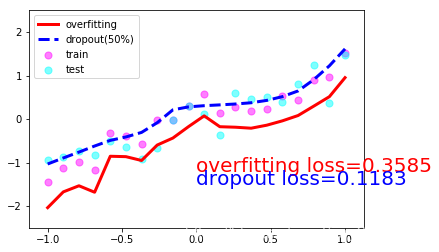
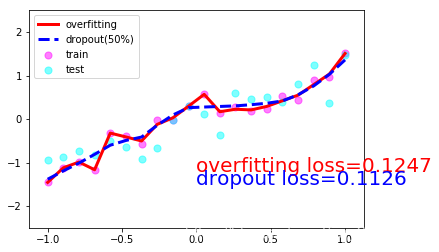
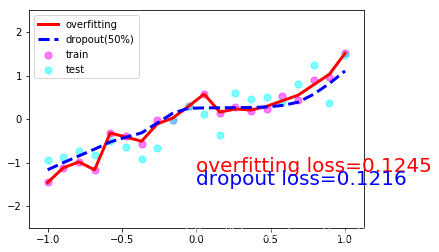
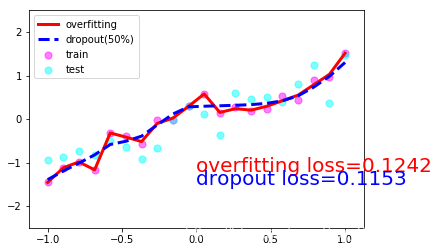
3. Dropout的numpy實現(xiàn)（參考斯坦福大學CS231n課程筆記）
網(wǎng)上對于為什么dropout后要進行rescale縮放的討論很多，這里給出斯坦福cs231n課上的解釋，個人覺得比較有道理，這里是對普通dropout的改進，使得無論是否使用隨機失活，預(yù)測方法的代碼可以保持不變。
一個3層神經(jīng)網(wǎng)絡(luò)的普通版dropout可以用下面代碼實現(xiàn)：
""" 普通版隨機失活: 不推薦實現(xiàn) """
p = 0.5 # 激活神經(jīng)元激活神經(jīng)元激活神經(jīng)元（重要的事情說三遍）的概率. p值更高 = 隨機失活更弱
def train_step(X):
""" X中是輸入數(shù)據(jù) """
# 3層neural network的前向傳播
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = np.random.rand(*H1.shape) p # 第一個dropout mask
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = np.random.rand(*H2.shape) p # 第二個dropout mask
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# 反向傳播:計算梯度... (略)
# 進行參數(shù)更新... (略)
def predict(X):
# 前向傳播時模型集成
H1 = np.maximum(0, np.dot(W1, X) + b1) * p # 注意：激活數(shù)據(jù)要乘以p
H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # 注意：激活數(shù)據(jù)要乘以p
out = np.dot(W3, H2) + b3
上述操作不好的性質(zhì)是必須在測試時對激活數(shù)據(jù)要按照 p 進行數(shù)值范圍調(diào)整，我們可以使其在訓練時就進行數(shù)值范圍調(diào)整，從而讓前向傳播在測試時保持不變。
這樣做還有一個好處，無論你決定是否使用隨機失活，預(yù)測方法的代碼可以保持不變。這就是反向隨機失活（inverted dropout）：
"""
inverted dropout（反向隨機失活）: 推薦實現(xiàn)方式.
在訓練的時候drop和調(diào)整數(shù)值范圍，測試時不用任何改變.
"""
p = 0.5 # 激活神經(jīng)元的概率. p值更高 = 隨機失活更弱
def train_step(X):
# 3層neural network的前向傳播
H1 = np.maximum(0, np.dot(W1, X) + b1)
U1 = (np.random.rand(*H1.shape) p) / p # 第一個dropout mask. 注意/p!
H1 *= U1 # drop!
H2 = np.maximum(0, np.dot(W2, H1) + b2)
U2 = (np.random.rand(*H2.shape) p) / p # 第二個dropout mask. 注意/p!
H2 *= U2 # drop!
out = np.dot(W3, H2) + b3
# 反向傳播:計算梯度... (略)
# 進行參數(shù)更新... (略)
def predict(X):
# 前向傳播時模型集成
H1 = np.maximum(0, np.dot(W1, X) + b1) # 不用數(shù)值范圍調(diào)整了
H2 = np.maximum(0, np.dot(W2, H1) + b2)
out = np.dot(W3, H2) + b3
以上為個人經(jīng)驗，希望能給大家一個參考，也希望大家多多支持腳本之家。
您可能感興趣的文章:- 淺談pytorch中的dropout的概率p
- pytorch 實現(xiàn)在測試的時候啟用dropout
- Python深度學習pytorch神經(jīng)網(wǎng)絡(luò)Dropout應(yīng)用詳解解
