在數(shù)字圖像中���,往往存在著一些特殊形狀的幾何圖形���,像檢測馬路邊一條直線,檢測人眼的圓形等等����,有時我們需要把這些特定圖形檢測出來,hough變換就是這樣一種檢測的工具��。
Hough變換的原理是將特定圖形上的點變換到一組參數(shù)空間上�,根據(jù)參數(shù)空間點的累計結(jié)果找到一個極大值對應(yīng)的解,那么這個解就對應(yīng)著要尋找的幾何形狀的參數(shù)(比如說直線�,那么就會得到直線的斜率k與常熟b,圓就會得到圓心與半徑等等)����。
關(guān)于hough變換,核心以及難點就是關(guān)于就是有原始空間到參數(shù)空間的變換上����。以直線檢測為例�,假設(shè)有一條直線L,原點到該直線的垂直距離為p����,垂線與x軸夾角為 θ ���,那么這條直線是唯一的,且直線的方程為 ρ=xcosθ+ysinθ , 如下圖所示:

可以看到的是這條直線在極坐標系下只有一個 (ρ,θ) 與之對應(yīng)����,隨便改變其中一個參數(shù)的大小,變換到空間域上的這個直線將會改變�����。好了�,再回來看看這個空間域上的這條直線上的所有點吧,你會發(fā)現(xiàn)����,這條直線上的所有點都可以是在極坐標為 (ρ,θ) 所表示的直線上的,為什么說是都可以在����,因為其中隨便的一個點也可以在其他的 (ρ,θ) 所表示的直線上,就比如上述的(x,y)吧�,它可以再很多直線上,準確的說,在經(jīng)過這個點的直線上���,隨便畫兩條如下:
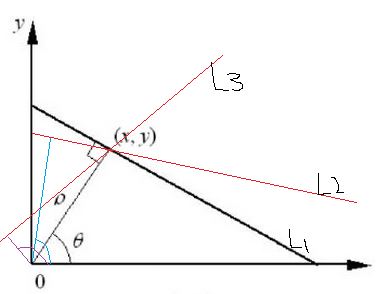
可以看到�����,光是空間上的一個點在極坐標系下就可能在很多極坐標對所對應(yīng)的直線上�����,具體有多少個極坐標對呢�����?那得看你的 θ 的步長了��,我們可以看到 θ 無非是從0-360度( 0−2π )變化��,假設(shè)我們沒10度一走取一個直線(這個點在這個直線上)�,那么我們走一圈是不是取了36條直線����,也就對應(yīng)36個極坐標對沒錯吧,那么這個極坐標對���,畫在坐標軸上是什么樣子的呢����?因為 θ 是從 0−2π �,并且一個點定了,如果一個 θ 也定了�����,你想想它對應(yīng)的直線的 ρ 會怎么樣����,自然也是唯一的。那么這個點在極坐標下對應(yīng)的 (ρ,θ) 畫出來一個周期可能就是這樣的����,以 θ 為x軸的話:

ok前面說的是單單這一個點對應(yīng)的極坐標系下的參數(shù)對,那么如果每個點都這么找一圈呢����?也就是每個點在參數(shù)空間上都對應(yīng)一系列參數(shù)對吧,現(xiàn)在把它們?nèi)A仔同一個坐標系下會怎么樣呢���?為了方便����,假設(shè)在這個直線上取3個點畫一下:
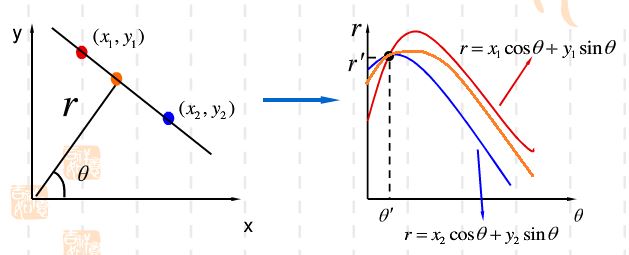
那么可以看到,首先對于每一個點��,在極坐標下��,會存在一個周期的曲線來表示通過這個點����,其次,這三個極坐標曲線同時經(jīng)過一個點����,要搞清楚的是,極坐標上每一個點對 (ρ,θ) 在空間坐標上都是對應(yīng)一條直線的���。好了��,同時經(jīng)過的這一個點有什么含義呢����?它表示在空間坐標系下��,有一條直線可以經(jīng)過點1�����,經(jīng)過點2,經(jīng)過點3����,這是什么意思�����?說明這三個點在一條直線上吧��。反過來再來看這個極坐標系下的曲線�,那么我們只需要找到交點最多的點,把它返回到空間域就是這個需要找的直線了��。為什么是找相交最多的點�����,因為上面這只是三個點的曲線���,當空間上很多點都畫出來的時候����,那么相交的點可能就不知上述看到的一個點了,可能有多個曲線相交點��,但是有一點�����,勢必是一條直線上的所有點匯成的交點是曲線相交次數(shù)最多的����。
再來分析這個算法?��?梢钥吹絟ough變換就是參數(shù)映射變換�����。對每一個點都進行映射���,并且每一個映射還不止一次, (ρ,θ) 都是存在步長的���,像一個點映射成一個 (ρ,θ) �����,以 θ 取步長為例�,當 θ 取得步長大的時候,映射的 (ρ,θ) 對少些��,反之則多��,但是我們有看到�����,映射后的點對是需要求交點的����,上述畫出來的曲線是連續(xù)的�,然而實際上因為 θ 步長的存在,他不可能是連續(xù)的��,像上上個圖一樣����,是離散的。那么當 θ 步長取得比較大的時候��,你還想有很多交點是不可能的��,因為這個時候是離散的曲線然后再去相交,所以說 θ 步長不能太大�,理論上是越小效果越好,因為越小�����,越接近于連續(xù)曲線��,也就越容易相交����,但是越小帶來的問題就是需要非常多的內(nèi)存,計算機不會有那么多內(nèi)存給你的����,并且越小,計算量越大�,想想一個點就需要映射那么多次,每次映射是需要計算的����,耗時的。那么再想想對于一副圖像所有點都進行映射����,隨便假設(shè)一副100*100的圖像(很小吧)����,就有10000個點�,對每個點假設(shè)就映射36組 (ρ,θ) 參數(shù)(此時角度的步長是10度了,10度�����,已經(jīng)非常大的一個概念了)���,那么總共需要映射360000次�,在考慮每次映射計算的時間吧�����?���?上攵?����,hough是多么耗時耗力�����。所以必須對其進行改進。首先就是對圖像進行改進��,100*100的圖像��,10000個點�,是不是每個點都要計算?大可不必���,我們只需要在開始把圖像進行一個輪廓提取��,一般使用canny算子就可以����,生成黑白二值圖像�����,白的是輪廓��,那么在映射的時候�,只需要把輪廓上的點進行參數(shù)空間變換,為什么提輪廓?想想無論檢測圖像中存在的直線呀圓呀�����,它們都是輪廓鮮明的�。那么需要變換的點可能就從10000個點降到可能1000個點了,這也就是為什么看到許多hough變換提取形狀時為什么要把圖像提取輪廓����,變成二值圖像了。
繼續(xù)算法��,分析這么多�����,可想而知那么一個hough變換在算法設(shè)計上就可以如下步驟:
(1)將參數(shù)空間 (ρ,θ) 量化���,賦初值一個二維矩陣M�, M(ρ,θ) 就是一個累加器了�����。
(2)然后對圖像邊界上的每一個點進行變換����,變換到屬于哪一組 (ρ,θ) ,就把該組 (ρ,θ) 對應(yīng)的累加器數(shù)加1���,這里的需要變換的點就是上面說的經(jīng)過邊緣提取以后的圖像了����。
(3)當所有點處理完成后�����,就來分析得到的 M(ρ,θ) �����,設(shè)置一個閾值T����,認為當 M(ρ,θ)>T ,就認為存在一條有意義的直線存在�����。而對應(yīng)的 M(ρ,θ) 就是這組直線的參數(shù)���,至于T是多少���,自己去式���,試的比較合適為止。
(4)有了 M(ρ,θ) 和點(x,y)計算出來這個直線就ok了�。
說了這么多,這就是原理上hough變換的最底層原理����,事實上完全可以自己寫程序去實現(xiàn)這些,然而�����,也說過�,hough變換是一個耗時耗力的算法,自己寫循環(huán)實現(xiàn)通常很慢����,曾經(jīng)用matlab寫過這個,也有實際的hough變換例子可以看看:
function mean_circle = hough_circle(BW,step_r,step_angle,r_min,r_max,p)
%------------------------------算法概述-----------------------------
% 該算法通過a = x-r*cos(angle)�,b = y-r*sin(angle)將圓圖像中的邊緣點
% 映射到參數(shù)空間(a,b,r)中���,由于是數(shù)字圖像且采取極坐標��,angle和r都取
% 一定的范圍和步長�����,這樣通過兩重循環(huán)(angle循環(huán)和r循環(huán))即可將原圖像
% 空間的點映射到參數(shù)空間中����,再在參數(shù)空間(即一個由許多小立方體組成的
% 大立方體)中尋找圓心,然后求出半徑坐標�。
%-------------------------------------------------------------------
%------------------------------輸入?yún)?shù)-----------------------------
% BW:二值圖像;
% step_r:檢測的圓半徑步長
% step_angle:角度步長����,單位為弧度 :各度計算 1° = 0.0174
% 2° = 0.035
% 3° = 0.0524
% 4° = 0.0698
% 5° = 0.0872
% r_min:最小圓半徑
% r_max:最大圓半徑
% p:以p*hough_space的最大值為閾值,p取0�����,1之間的數(shù)
%-------------------------------------------------------------------
% --------對半徑的大小范圍規(guī)定問題--------
% ------ 實驗中發(fā)現(xiàn):外輪廓的半徑范圍在220~260之間
% 內(nèi)輪廓的半徑范圍 60~80之間
% Note:: 當圖像改變時半徑范圍需要改變
% question: 半徑的范圍差超過50將會顯示內(nèi)存不足����,注意方案辦法
%------------------------------輸出參數(shù)-----------------------------
% hough_space:參數(shù)空間,h(a,b,r)表示圓心在(a,b)半徑為r的圓上的點數(shù)
% hough_circl:二值圖像�,檢測到的圓
% para:檢測到的所有圓的圓心�、半徑
% mean_circle : 返回檢測到的圓的平均位置及大小
%-------------------------------------------------------------------
[m,n] = size(BW); %取大小
size_r = round((r_max-r_min)/step_r)+1; %半徑增加�����,循環(huán)次數(shù)
size_angle = round(2*pi/step_angle); %角度增加����,循環(huán)次數(shù)
hough_space = zeros(m,n,size_r); %hough空間
[rows,cols] = find(BW);%把要檢測的點存起來���,只有白色(邊緣)點需要變換
ecount = size(rows); %檢測的點的個數(shù)
tic %%%% 計時開始位置
% Hough變換
% 將圖像空間(x,y)對應(yīng)到參數(shù)空間(a,b,r)
% a = x-r*cos(angle)
% b = y-r*sin(angle)
for i=1:ecount %點個數(shù)循環(huán)
for r=1:size_r %單個點在所有半徑空間內(nèi)檢測
for k=1:size_angle %單個點在半徑一定的所在圓內(nèi)檢測
a = round(rows(i)-(r_min+(r-1)*step_r)*cos(k*step_angle));
b = round(cols(i)-(r_min+(r-1)*step_r)*sin(k*step_angle));
if(a>0a=mb>0b=n) %對應(yīng)到某個圓上�����,記錄之
hough_space(a,b,r) = hough_space(a,b,r)+1;
end
end
end
end
% 搜索超過閾值的聚集點
max_para = max(max(max(hough_space)));%找到最大值所在圓參數(shù)
index = find(hough_space>=max_para*p);%索引在一定范圍內(nèi)的圓參數(shù)
length = size(index);
toc %%%% 計時結(jié)束位置�����,通過計時觀察運行效率,hough變換的一大缺點就是耗時
% 將索引結(jié)果轉(zhuǎn)換為對應(yīng)的行列(圓心)和半徑大小
% 理解三維矩陣在內(nèi)存中的存儲方式可以理解公式的原理
for k=1:length
par3 = floor(index(k)/(m*n))+1;
par2 = floor((index(k)-(par3-1)*(m*n))/m)+1;%轉(zhuǎn)換為圓心的y值
par1 = index(k)-(par3-1)*(m*n)-(par2-1)*m;%轉(zhuǎn)換為圓心的x值
par3 = r_min+(par3-1)*step_r; %轉(zhuǎn)化為圓的半徑
%儲存在一起
para(:,k) = [par1,par2,par3]';
end
% 為提高準確性�����,求取一個大致的平均位置(而不是直接采用的最大值)
mean_circle = round(mean(para')');
那么我們在實際中大可不必自己寫,opencv已經(jīng)集成了hough變換的函數(shù)���,調(diào)用它的函數(shù)效率高���,也很簡單��。
Opencv中檢測直線的函數(shù)有cv2.HoughLines(),cv2.HoughLinesP()
函數(shù)cv2.HoughLines()返回值有三個(opencv 3.0)�,實際是個二維矩陣,表述的就是上述的 (ρ,θ) ���,其中 ρ 的單位是像素長度(也就是直線到圖像原點(0,0)點的距離)��,而 θ 的單位是弧度����。這個函數(shù)有四個輸入�,第一個是二值圖像,上述的canny變換后的圖像����,二三參數(shù)分別是 ρ 和 θ 的精確度,可以理解為步長��。第四個參數(shù)為閾值T���,認為當累加器中的值高于T是才認為是一條直線����。自己畫了個圖實驗一下:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('line.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)#灰度圖像
#open to see how to use: cv2.Canny
#http://blog.csdn.net/on2way/article/details/46851451
edges = cv2.Canny(gray,50,200)
plt.subplot(121),plt.imshow(edges,'gray')
plt.xticks([]),plt.yticks([])
#hough transform
lines = cv2.HoughLines(edges,1,np.pi/180,160)
lines1 = lines[:,0,:]#提取為為二維
for rho,theta in lines1[:]:
a = np.cos(theta)
b = np.sin(theta)
x0 = a*rho
y0 = b*rho
x1 = int(x0 + 1000*(-b))
y1 = int(y0 + 1000*(a))
x2 = int(x0 - 1000*(-b))
y2 = int(y0 - 1000*(a))
cv2.line(img,(x1,y1),(x2,y2),(255,0,0),1)
plt.subplot(122),plt.imshow(img,)
plt.xticks([]),plt.yticks([])
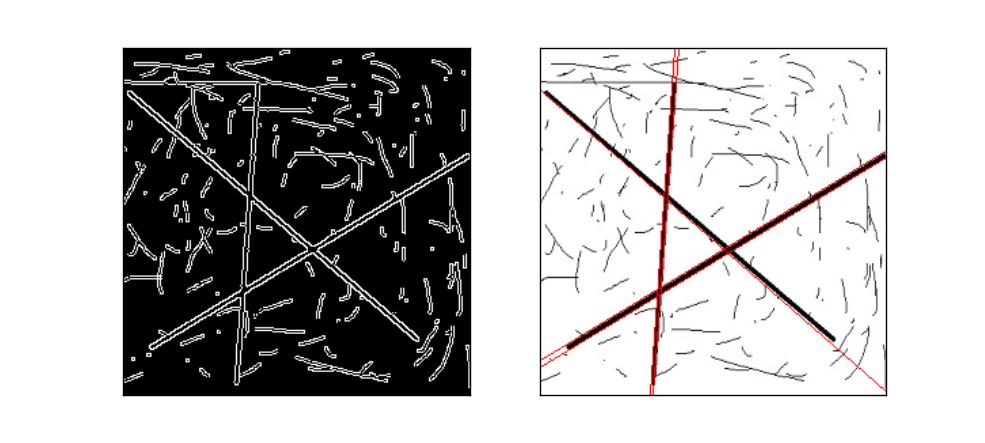
測試一個新的圖��,不停的改變 cv2.HoughLines最后一個閾值參數(shù)到合理的時候如下:
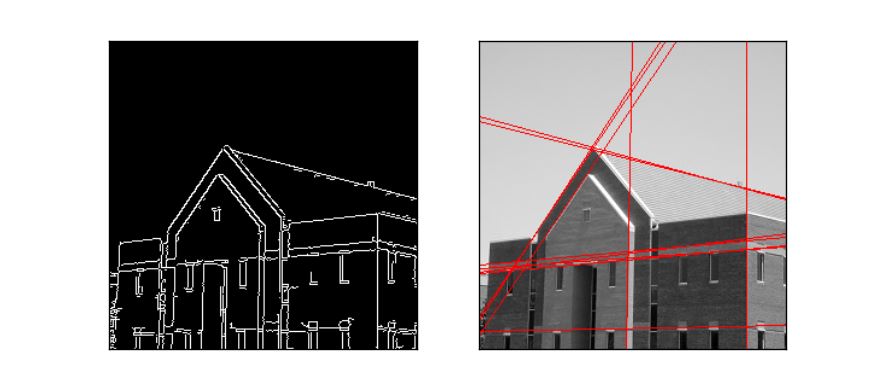
可以看到檢測的還可以的���。
函數(shù)cv2.HoughLinesP()是一種概率直線檢測�,我們知道���,原理上講hough變換是一個耗時耗力的算法�����,尤其是每一個點計算�����,即使經(jīng)過了canny轉(zhuǎn)換了有的時候點的個數(shù)依然是龐大的�,這個時候我們采取一種概率挑選機制,不是所有的點都計算�,而是隨機的選取一些個點來計算,相當于降采樣了���。這樣的話我們的閾值設(shè)置上也要降低一些���。在參數(shù)輸入輸出上����,輸入不過多了兩個參數(shù):minLineLengh(線的最短長度,比這個短的都被忽略)和MaxLineCap(兩條直線之間的最大間隔�,小于此值,認為是一條直線)�。輸出上也變了,不再是直線參數(shù)的�,這個函數(shù)輸出的直接就是直線點的坐標位置,這樣可以省去一系列for循環(huán)中的由參數(shù)空間到圖像的實際坐標點的轉(zhuǎn)換����。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('room.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)#灰度圖像
#open to see how to use: cv2.Canny
#http://blog.csdn.net/on2way/article/details/46851451
edges = cv2.Canny(gray,50,200)
plt.subplot(121),plt.imshow(edges,'gray')
plt.xticks([]),plt.yticks([])
#hough transform
lines = cv2.HoughLinesP(edges,1,np.pi/180,30,minLineLength=60,maxLineGap=10)
lines1 = lines[:,0,:]#提取為二維
for x1,y1,x2,y2 in lines1[:]:
cv2.line(img,(x1,y1),(x2,y2),(255,0,0),1)
plt.subplot(122),plt.imshow(img,)
plt.xticks([]),plt.yticks([])
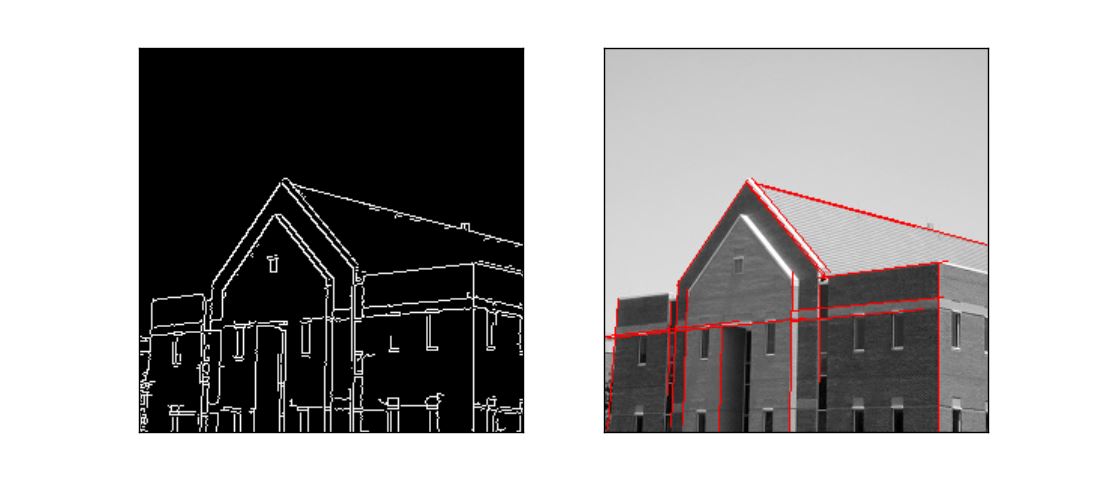
可以看到這個方法似乎更好些,速度還快�,調(diào)參數(shù)得到較好的效果就ok了。
Ok說完了直線的檢測�,再來說說圓環(huán)的檢測����,我們知道圓的數(shù)學(xué)表示為:

從而一個圓的確定需要三個參數(shù)����,那么就需要三層循環(huán)來實現(xiàn)(比直線的多一層),從容把圖像上的所有點映射到三維參數(shù)空間上�。其他的就一樣了,尋找參數(shù)空間累加器的最大(或者大于某一閾值)的值��。那么理論上圓的檢測將比直線更耗時��,然而opencv對其進行了優(yōu)化�,用了一種霍夫梯度法,感興趣去研究吧����,我們只要知道它能優(yōu)化算法的效率就可以了。關(guān)于函數(shù)參數(shù)輸入輸出:
cv2.HoughCircles(image, method, dp, minDist, circles, param1, param2, minRadius, maxRadius)
這個時候輸入為灰度圖像�,同時最好規(guī)定檢測的圓的最大最小半徑,不能盲目的檢測����,否側(cè)浪費時間空間。輸出就是三個參數(shù)空間矩陣。
來個實際點的人眼圖像�,把minRadius和maxRadius調(diào)到大圓范圍檢測如下:
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('eye.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)#灰度圖像
plt.subplot(121),plt.imshow(gray,'gray')
plt.xticks([]),plt.yticks([])
#hough transform
circles1 = cv2.HoughCircles(gray,cv2.HOUGH_GRADIENT,1,
100,param1=100,param2=30,minRadius=200,maxRadius=300)
circles = circles1[0,:,:]#提取為二維
circles = np.uint16(np.around(circles))#四舍五入�����,取整
for i in circles[:]:
cv2.circle(img,(i[0],i[1]),i[2],(255,0,0),5)#畫圓
cv2.circle(img,(i[0],i[1]),2,(255,0,255),10)#畫圓心
plt.subplot(122),plt.imshow(img)
plt.xticks([]),plt.yticks([])
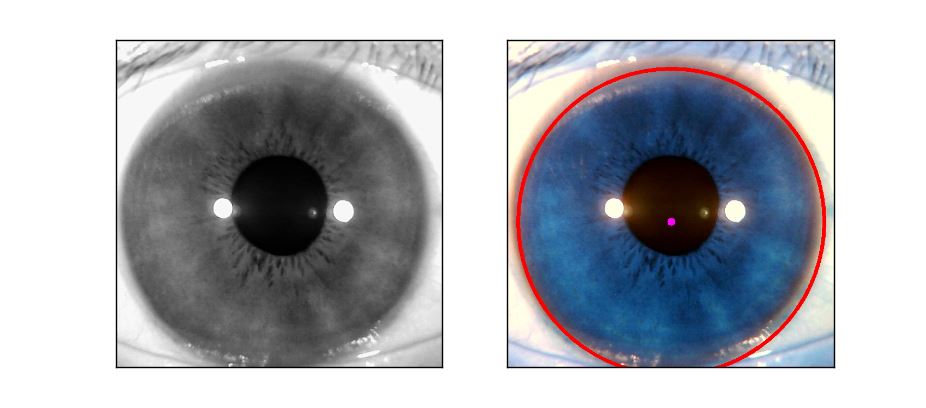
把半徑范圍調(diào)小點�����,檢測內(nèi)圓:
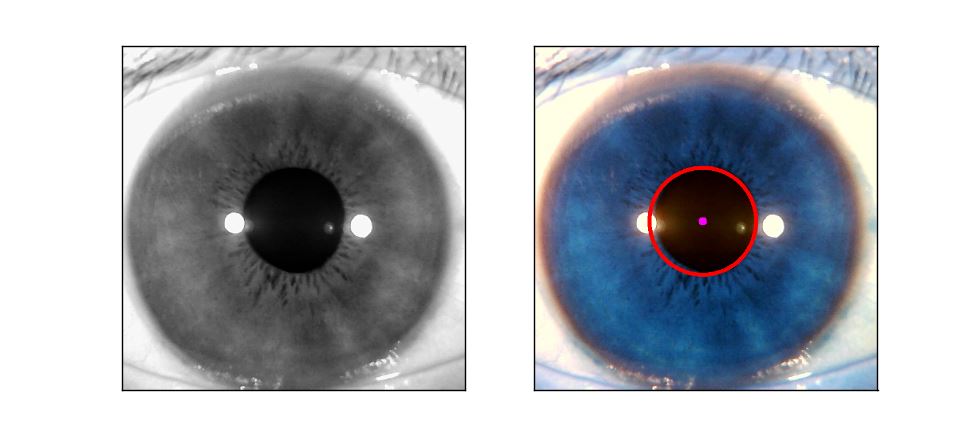
至此圓的檢測就是這樣��。
到此這篇關(guān)于Python下opencv使用hough變換檢測直線與圓的文章就介紹到這了,更多相關(guān)opencv hough變換檢測直線與圓內(nèi)容請搜索腳本之家以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持腳本之家��!
您可能感興趣的文章:- python opencv檢測直線 cv2.HoughLinesP的實現(xiàn)
- Opencv2.4.9函數(shù)HoughLinesP分析
- OpenCV霍夫變換(Hough Transform)直線檢測詳解
- Opencv Hough算法實現(xiàn)圖片中直線檢測
- 利用Opencv中Houghline方法實現(xiàn)直線檢測
- Java+opencv3.2.0實現(xiàn)hough直線檢測
- Java+opencv3.2.0實現(xiàn)hough圓檢測功能