目錄
- 一����、求解方法、算法和編程方案
- 1.1�、線性規(guī)劃問題的求解方法
- 1.2、線性規(guī)劃的最快算法
- 1.3�����、選擇適合自己的編程方案
- 二��、PuLP庫求解線性規(guī)劃問題
- 2.1��、線性規(guī)劃問題的描述
- 2.2���、PuLP 求解線性規(guī)劃問題的步驟
- 2.3�����、Python例程:線性規(guī)劃問題
- 三����、小結
一�、求解方法、算法和編程方案
線性規(guī)劃 (Linear Programming,LP) 是很多數(shù)模培訓講的第一個算法���,算法很簡單�,思想很深刻�����。
線性規(guī)劃問題是中學數(shù)學的內(nèi)容����,雞兔同籠就是一個線性規(guī)劃問題。數(shù)學規(guī)劃的題目在高考中也經(jīng)常出現(xiàn)�����,有直接給出線性約束條件求線性目標函數(shù)極值���,有間接給出約束條件求線性目標函數(shù)極值,還有已知約束條件求非線性目標函數(shù)極值問題���。
因此�����,線性規(guī)劃在數(shù)學建模各類問題和算法中確實是比較簡單的問題����。下面我們通過這個比較簡單、也比較熟悉的問題�����,分析一下數(shù)學模型問題的方法��、算法和學習方案�����。探討這些容易混淆的概念����,也便于大家理解本系列教程的初衷和特色。
1.1��、線性規(guī)劃問題的求解方法
解決線性規(guī)劃問題有很多數(shù)學方法�����,例如:
- 圖解法��, 用幾何作圖的方法并求出其最優(yōu)解,中學就講過這種方法�����,在經(jīng)濟學研究中十分常用�;
- 矩陣法, 引進松弛變量將線性規(guī)劃問題轉換成增廣矩陣形式后逐次求解�����, 是單純性法之前的典型方法�;
- 單純性法, 利用多面體在可行域內(nèi)逐步構造新的頂點來不斷逼近最優(yōu)解�,是線性規(guī)劃研究的里程碑,至今仍然是最重要的方法之一�;
- 內(nèi)點法,通過選取可行域內(nèi)部點沿下降方向不斷迭代來達到最優(yōu)解�����,是目前理論上最好的線性規(guī)劃問題求解方法�;
- 啟發(fā)式方法���,依靠經(jīng)驗準則不斷迭代改進來搜索最優(yōu)解 ���,如貪心法�、模擬退火����、遺傳算法、神經(jīng)網(wǎng)絡��。
雖然不同的求解方法都是面對線性規(guī)劃問題�,也就必然會殊途同歸,但它們在思想上就存在著本質區(qū)別���,在求解方法和步驟上也就完全不同�。
不夸張地說���,對于很多小白���,學沒學過單純性法,對于學習啟發(fā)式方法可能完全沒有區(qū)別�����。
這意味著什么呢��?這就是說,對于非數(shù)學專業(yè)的同學�����,對于學習數(shù)學建模的同學�����,針對每一類問題�,完全沒必要學習各種解決方法。即便是數(shù)學專業(yè)的同學��,也不可能在數(shù)模學習期間把各種方法都學會���。
對于小白�����,本文推薦選擇較為通用��、相對簡單(思路簡單���、程序簡單)的方法來進行學習�����,沒必要貪多求新。
1.2���、線性規(guī)劃的最快算法
算法�����,跟方法有什么不同呢��?
算法的定義是“解題方案的準確而完整的描述”��,是一系列解決問題的清晰指令����,算法代表著用系統(tǒng)的方法描述解決問題的策略機制����。
我對“方法”的理解是思想方法,是求解問題總體框架��,而“算法”是具體和明確的實現(xiàn)步驟�,在計算機編程中相當于詳細的流程圖。
在每一種方法的基本思想和方案提出后�����,往往都會有很多變形、改進和發(fā)展的算法�����。極少的改進算法具有實質貢獻而成為主流的經(jīng)典算法�����,即便如此往往也只是性能�����、效率上的提升�����,對于求解數(shù)模競賽中的問題基本沒有影響��。
而絕大多數(shù)改進算法只是針對某些特殊情況���、特殊問題(自稱)有效�����,常用于大量的灌水論文��。對于數(shù)學建模來說��,學習基本算法或者目前的經(jīng)典算法就足夠了�,不需要聽信改進算法中自稱的優(yōu)點����,那都是莆田系的廣告。
有一種例外情況�,就是一些算法是有適用范圍和限制條件的。舉個例子���,內(nèi)點法的基本算法不能處理等式約束�����,最短路徑問題中 Dijkstar算法不能處理負權邊�。這種情況下如果選錯算法����,問題是無法求解的。所以對我們來說,搞清楚算法的適用范圍����,比理解算法本身更重要。
回到本節(jié)的標題��,對于線性規(guī)劃問題����,什么算法是最快的呢?答案是:猜����。不是讓你猜,而是說求解線性規(guī)劃問題���,猜起來比較快��。不是開玩笑���,我是認真的。
佐治亞理工學院彭泱教授在 2021年計算機理論頂會 SODA2021 獲得最佳論文(Best paper award at ACM-SIAM symposium on discrete algorithms 2021)��,正是研究線性規(guī)劃問題的求解——“Solving sparse linear systems faster than matrix multiplication”���,所用的全新思路是:猜����,反復猜,迭代猜����。
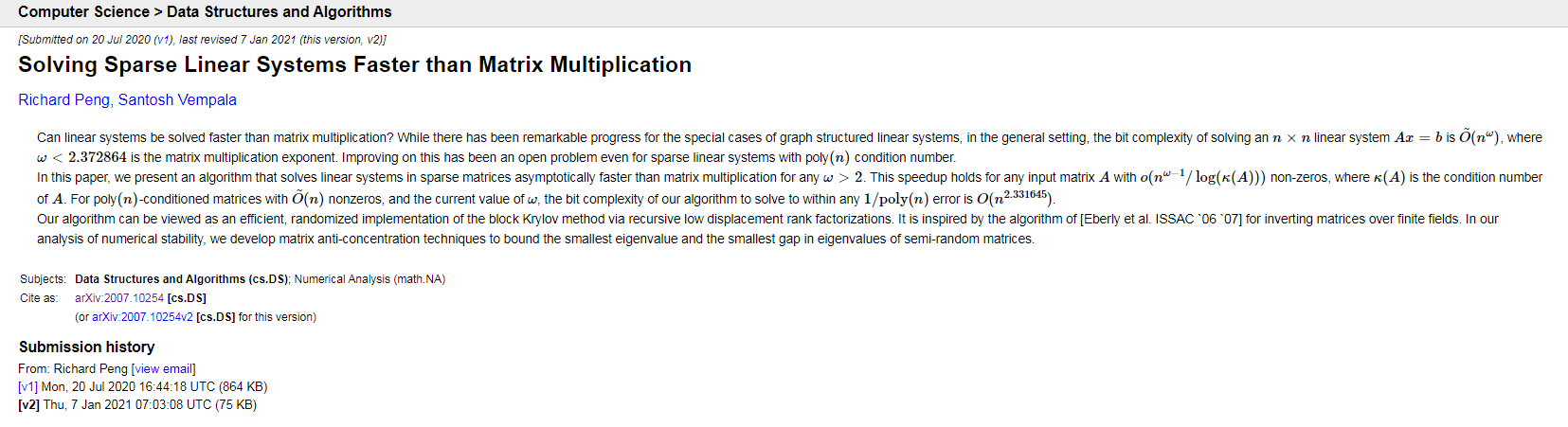
當然���,猜起來比較快只是在某些特殊條件下才有效的���,至于在什么條件下猜,怎么猜�����,這不是我們所要關心��,所能理解的問題了����。只是以此說明,簡單的問題也有復雜的情況��,每個問題都有很多求解的思路、方法和算法�。
1.3、選擇適合自己的編程方案
編程方案是我杜撰的術語��。我所要表達意思是�,在選擇了求解方法和算法以后,是自己按照算法步驟一步步編程實現(xiàn)��,或者找到例程調試使用�,還是調用第三方工具包/庫函數(shù)來完成呢?
首先�����,對于學習數(shù)學建模���、參加數(shù)模競賽��,不建議自己按照算法步驟去編程����。我們在《01.新手必讀》中討論過這個問題����,對于數(shù)學小白兼計算機小白�,這樣做既不可行也沒必要���;即使你愿意挑戰(zhàn)自我去試試�����,那其實已經(jīng)是走在學習另一門計算機或算法課程的路上了�。
其次���,要不要找到例程自己調試、使用��?很多數(shù)模培訓就是這么說��,這么做的���,而且把這些收集的例程當作核心機密吸引同學���。我不反對這樣做,這種學習方法對于理解算法���、提高編程能力很有幫助���;但是并不推薦這樣做�����,原因是:
(1)我認為學習數(shù)學建模����、參加數(shù)模競賽�����,重點應該放在識別問題��、分析問題���、解決問題�,能使用算法和編程就足夠了�����;
(2)第三方庫與例程沒有本質區(qū)別�����,第三方庫就是經(jīng)典的、規(guī)范的����、標準化的例程,既然選擇例程為什么不選擇優(yōu)秀的例程——第三方庫呢�?
(3)大部分例程都存在很多問題,即使調試通過仍然有很多坑�,而且新手難以識別。
所以我是明確推薦優(yōu)選直接使用第三方庫來解決問題,這也是 Python 語言“不要重復造輪子”的思想。
進一步地�,很多工具包/庫函數(shù)都能實現(xiàn)常用的算法��,應該如何選擇呢?
如果你對某個工具包已經(jīng)很熟悉��,又能實現(xiàn)所要的算法�����,這當然是理想的選擇。如果你是小白��,就跟著我走吧�。
本系列選擇第三方工具包的原則是:
(1)優(yōu)選常用的工具包;
(2)優(yōu)選通用功能的工具包和函數(shù)(例如��,最好既能實現(xiàn)線性規(guī)劃,又能實現(xiàn)整數(shù)規(guī)劃����、非線性規(guī)劃);
(3)優(yōu)選安裝簡單��、使用簡單�����、配置靈活的工具包���;
(4)優(yōu)選兼模型檢驗����、圖形繪制的工具包��。
二���、PuLP庫求解線性規(guī)劃問題
2.1����、線性規(guī)劃問題的描述
線性規(guī)劃是研究線性等式或不等式約束條件下求解線性目標函數(shù)的極值問題��,常用于解決資源分配、生產(chǎn)調度和混合問題���。
一般線性規(guī)劃問題的標準形式為:
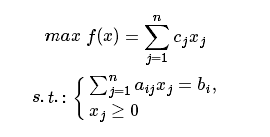
滿足所有約束條件的解�,稱為線性規(guī)劃問題的可行解�����;所有可行解構成的集合����,稱為可行域。
使目標函數(shù)達到最小值的解����,稱為最優(yōu)解。
線性規(guī)劃問題的建模和求解�,通常按照以下步驟進行:
- 問題定義,確定決策變量�、目標函數(shù)和約束條件�����;
- 模型構建���,由問題描述建立數(shù)學方程�,并轉化為標準形式的數(shù)學模型;
- 模型求解��,用標準模型的優(yōu)化算法對模型求解����,得到優(yōu)化結果。
很多 Python 的第三方包�����,都提供求解線性規(guī)劃問題的算法���,有的工具包還提供整數(shù)規(guī)劃��、非線性規(guī)劃的算法��。例如:
- Scipy 庫提供了解簡單線性或非線性規(guī)劃問題�����,但是不能求解如背包問題的0-1規(guī)劃問題��,或整數(shù)規(guī)劃問題�����,混合整數(shù)規(guī)劃問題�。
- PuLP 可以求解線性規(guī)劃、整數(shù)規(guī)劃�、0-1規(guī)劃、混合整數(shù)規(guī)劃問題��,提供多種針對不同類型問題的求解器�����。
- Cvxpy 是一種凸優(yōu)化工具包�����,可以求解線性規(guī)劃���、整數(shù)規(guī)劃��、0-1規(guī)劃�����、混合整數(shù)規(guī)劃����、二次規(guī)劃和幾何規(guī)劃問題�。
此外,SKlearn����、DOcplex、Pymprog 等很多第三方工具包也都能求解線性規(guī)劃問題��。
2.2����、PuLP 求解線性規(guī)劃問題的步驟
例題 1:
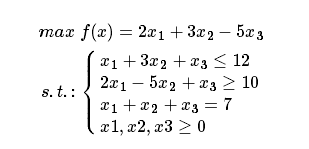
下面以該題為例講解 PuLP 求解線性規(guī)劃問題的步驟:
(0)導入 PuLP庫函數(shù)
(1)定義一個規(guī)劃問題
MyProbLP = pulp.LpProblem("LPProbDemo1", sense=pulp.LpMaximize)
pulp.LpProblem 是定義問題的構造函數(shù)。
"LPProbDemo1"是用戶定義的問題名(用于輸出信息)�����。
參數(shù) sense 用來指定求最小值/最大值問題����,可選參數(shù)值:LpMinimize、LpMaximize �����。本例 “sense=pulp.LpMaximize” 表示求目標函數(shù)的最大值。
(2)定義決策變量
x1 = pulp.LpVariable('x1', lowBound=0, upBound=7, cat='Continuous')
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7, cat='Continuous')
x3 = pulp.LpVariable('x3', lowBound=0, upBound=7, cat='Continuous')
pulp.LpVariable 是定義決策變量的函數(shù)��。
'x1' 是用戶定義的變量名�。
參數(shù) lowBound、upBound 用來設定決策變量的下界�����、上界���;可以不定義下界/上界�,默認的下界/上界是負無窮/正無窮����。本例中 x1,x2,x3 的取值區(qū)間為 [0,7]。
參數(shù) cat 用來設定變量類型�,可選參數(shù)值:'Continuous' 表示連續(xù)變量(默認值)、' Integer ' 表示離散變量(用于整數(shù)規(guī)劃問題)�����、' Binary ' 表示0/1變量(用于0/1規(guī)劃問題)�。
(3)添加目標函數(shù)
MyProbLP += 2*x1 + 3*x2 - 5*x3 # 設置目標函數(shù)
添加目標函數(shù)使用 "問題名 += 目標函數(shù)式" 格式�����。
(4)添加約束條件
MyProbLP += (2*x1 - 5*x2 + x3 >= 10) # 不等式約束
MyProbLP += (x1 + 3*x2 + x3 = 12) # 不等式約束
MyProbLP += (x1 + x2 + x3 == 7) # 等式約束
添加約束條件使用 "問題名 += 約束條件表達式" 格式����。
約束條件可以是等式約束或不等式約束��,不等式約束可以是 小于等于 或 大于等于���,分別使用關鍵字">="、"="和"=="��。
(5)求解
MyProbLP.solve()
print("Status:", pulp.LpStatus[MyProbLP.status]) # 輸出求解狀態(tài)
for v in MyProbLP.variables():
print(v.name, "=", v.varValue) # 輸出每個變量的最優(yōu)值
print("F(x) = ", pulp.value(MyProbLP.objective)) #輸出最優(yōu)解的目標函數(shù)值
solve() 是求解函數(shù)����。PuLP默認采用 CBC 求解器來求解優(yōu)化問題,也可以調用其它的優(yōu)化器來求解����,如:GLPK,COIN CLP/CBC��,CPLEX����,和GUROBI����,但需要另外安裝����。
2.3�����、Python例程:線性規(guī)劃問題
例程 1:求解線性規(guī)劃問題
import pulp
MyProbLP = pulp.LpProblem("LPProbDemo1", sense=pulp.LpMaximize) # 求最大值
x1 = pulp.LpVariable('x1', lowBound=0, upBound=7, cat='Continuous')
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7, cat='Continuous')
x3 = pulp.LpVariable('x3', lowBound=0, upBound=7, cat='Continuous')
MyProbLP += 2*x1 + 3*x2 - 5*x3 # 設置目標函數(shù)
MyProbLP += (2*x1 - 5*x2 + x3 >= 10) # 不等式約束
MyProbLP += (x1 + 3*x2 + x3 = 12) # 不等式約束
MyProbLP += (x1 + x2 + x3 == 7) # 等式約束
MyProbLP.solve() # youcans@xupt
print("Status:", pulp.LpStatus[MyProbLP.status]) # 輸出求解狀態(tài)
for v in MyProbLP.variables(): # youcans
print(v.name, "=", v.varValue) # 輸出每個變量的最優(yōu)值
print("Max F(x) = ", pulp.value(MyProbLP.objective)) #輸出最優(yōu)解的目標函數(shù)值
例程 1 運行結果:
Welcome to the CBC MILP Solver
Version: 2.9.0
Build Date: Feb 12 2015
Status: Optimal
x1 = 6.4285714
x2 = 0.57142857
x3 = 0.0
Max F(x) = 14.57142851
例程01 程序說明:
- 用 PuLP 庫求解線性規(guī)劃問題���,可以選擇求最大值或最小值�,可以按照問題的數(shù)學描述�,直接輸入目標函數(shù)、等式約束和不等式約束���,不等式約束可以選擇 = 或 >=�����,不需要進行轉換����。這中方式簡單直觀,非常適合初學者掌握�。
- 對于較大規(guī)模線性規(guī)劃問題, PuLP 庫支持用字典類型(dict)建立多個變量���,設置目標函數(shù)和約束條件��。
三、小結
求解線性規(guī)劃問題的方法非常簡單���,本文實際上并未講解具體的算法���。
希望通過對求解方法、算法和編程方案的講解�,闡明作者對于數(shù)學建模學什么、怎么學的理解�,也使讀者能了解本系列教程的特點:本教程不打算詳細講解各種算法的具體方法,重點介紹如何使用第三方包實現(xiàn)算法�、解決問題。
以上就是淺談Python數(shù)學建模之線性規(guī)劃的詳細內(nèi)容�,更多關于Python 線性規(guī)劃的資料請關注腳本之家其它相關文章!
您可能感興趣的文章:- Python小白必備的8個最常用的內(nèi)置函數(shù)(推薦)
- 小白入門篇使用Python搭建點擊率預估模型
- 深入解析Python小白學習【操作列表】
- 初學python數(shù)學建模之數(shù)據(jù)導入(小白篇)