目錄
- 1.審查分類算法
- 1.1線性算法審查
- 1.2非線性算法審查
- 1.2.1K近鄰算法
- 1.2.2貝葉斯分類器
- 1.2.3分類與回歸樹
- 1.2.4支持向量機
- 2.審查回歸算法
- 2.1線性算法審查
- 2.1.1線性回歸算法
- 2.1.2嶺回歸算法
- 2.1.3套索回歸算法
- 2.1.4彈性網(wǎng)絡回歸算法
- 2.2非線性算法審查
- 2.2.1K近鄰算法
- 2.2.2分類與回歸樹
- 2.2.3支持向量機
- 3.算法比較
- 總結(jié)
程序測試是展現(xiàn)BUG存在的有效方式����,但令人絕望的是它不足以展現(xiàn)其缺位。
——艾茲格·迪杰斯特拉(Edsger W. Dijkstra)
算法審查時選擇合適的機器學習算法主要方式之一�。審查算法前并不知道哪個算法對問題最有效,必須設計一定的實驗進行驗證�����,以找到對問題最有效的算法����。
審查算法前沒有辦法判斷那個算法對數(shù)據(jù)集最有效、能夠生成最優(yōu)模型���,必須通過一些列的實驗進行驗證才能夠得出結(jié)論����,從而選擇最優(yōu)的算法���。這個過程被稱為審查算法���。
審查算法時�,要嘗試多種代表性算法���、機器學習算法以及多種模型���,通過大量實驗才能找到最有效的算法。
1.審查分類算法
1.1線性算法審查
1.1.1邏輯回歸
邏輯回歸其實是一個分類算法而不是回歸算法���,通常是利用已知的自變量來預測一個離散型因變量的值(如二進制0/1、真/假)�����。簡單來說�����,它就是通過擬合一個邏輯回歸函數(shù)(Logistic Function)來預測事件發(fā)生的概率��。所以它預測的是一個概率值��,它的輸出值應該為0~1���,因此非常適合二分類問題�。
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression#邏輯回歸
filename = 'pima_data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(filename, names=names)
array = data.values
X = array[:, 0:8]
Y = array[:, 8]
#邏輯回歸
num_folds = 10
seed = 7
kfold = KFold(n_splits=num_folds, random_state=seed, shuffle=True)
model = LogisticRegression(max_iter=3000)
result = cross_val_score(model, X, Y, cv=kfold)
print(result.mean())
執(zhí)行結(jié)果如下:0.7721633629528366
1.1.2線性判別分析
線性判別分析(Linear DIscriminant Analysis,LDA)�����,也叫做Fisher線性判別(Fisher Linear Discriminant Analysis���,F(xiàn)LD)���。它的思想是將高維的模式樣本投影到最佳鑒別矢量空間,以達到抽取分類信息和壓縮特征空間維數(shù)的效果���,投影后保證模式樣本在新的子空間有最大類間距離和最小類內(nèi)距離�����。因此����,他是一種有效的特征抽取方法��。(完全不懂它是什么東西�。。。)
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
#相同代碼不再贅述
#線性判別分析
model = LinearDiscriminantAnalysis()
result = cross_val_score(model, X, Y, cv=kfold)
print(result.mean())
執(zhí)行結(jié)果如下:
0.7669685577580315
1.2非線性算法審查
1.2.1K近鄰算法
K近鄰算法的基本思路是:如果一個樣本在特征空間中的k個最相似的樣本中大多數(shù)屬于某一個類別�����,則該樣本也屬于這個了類別����。在scikit-learn中通過KNeighborsClassifier實現(xiàn)。
from sklearn.neighbors import KNeighborsClassifier
#相同代碼不再贅述
#K近鄰
model = KNeighborsClassifier()
result = cross_val_score(model, X, Y,cv=kfold)
print(result.mean())
0.7109876965140123
1.2.2貝葉斯分類器
貝葉斯分類器的分類原理是通過某對象的先驗概率�����,利用貝葉斯公式計算出其在所有類別上的后驗概率���,即該對象屬于某一類的來率,選擇具有最大后驗概率的類作為該對象所屬的類�。
from sklearn.naive_bayes import GaussianNB
#貝葉斯分類器
model = GaussianNB()
result = cross_val_score(model, X, Y,cv=kfold)
print(result.mean())
0.7591421736158578
1.2.3分類與回歸樹
分類與回歸樹(CART).CART算法由以下兩布組成:
- 樹的生成:基于訓練集生成決策樹,生成的決策樹要盡量大���。
- 樹的剪枝:用驗證集對已生成的樹進行剪枝��,并選擇最優(yōu)子樹�,這時以損失函數(shù)最小作為剪枝標準�����。
from sklearn.tree import DecisionTreeClassifier
#分類與回歸樹
model = DecisionTreeClassifier()
result = cross_val_score(model, X, Y,cv=kfold)
print(result.mean())
0.688961038961039
1.2.4支持向量機
from sklearn.svm import SVC
#支持向量機
model = SVC()
result = cross_val_score(model, X, Y,cv=kfold)
print(result.mean())
0.760457963089542
2.審查回歸算法
本部分使用波士頓房價的數(shù)據(jù)集來審查回歸算法,采用10折交叉驗證來分離數(shù)據(jù)��,并應用到所有的算法上����。
2.1線性算法審查
2.1.1線性回歸算法
線性回歸算法時利用數(shù)理統(tǒng)計中的回歸分析,來確定兩種或兩種以上變量間相互依賴的定量關系的一種統(tǒng)計分析方法�����。在回歸分析中���,若只包含一個自變量和一個因變量����,且二者的關系可用一條直線近似表示�����,這種回歸分析成為一元線性回歸分析���。如果回歸分析中包含兩個或兩個以上的自變量�,且因變量和自變量之間是線性關系,則稱為多元線性回歸分析�����。
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
filename = 'housing.csv'
names = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PRTATIO','B','LSTAT','MEDV']
data = read_csv(filename,names=names,delim_whitespace=True)
array = data.values
X = array[:,0:13]
Y = array[:,13]
n_splits = 10
seed = 7
kfold = KFold(n_splits=n_splits,random_state=seed,shuffle=True)
#線性回歸算法
model = LinearRegression()
scoring = 'neg_mean_squared_error'
result = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("線性回歸算法:%.3f" % result.mean())
線性回歸算法:-23.747
2.1.2嶺回歸算法
嶺回歸算法是一種專門用于共線性數(shù)據(jù)分析的有偏估計回歸方法�����,實際上是一種改良的最小二乘估計法�����,通過放棄最小二乘法的無偏性���,以損失部分信息���、降低精度為代價,獲得回歸系數(shù)更符合實際����、更可靠的回歸方法�����,對病態(tài)數(shù)據(jù)的擬合要強于最小二乘法。
from sklearn.linear_model import Ridge
#嶺回歸算法
model = Ridge()
scoring = 'neg_mean_squared_error'
result = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("嶺回歸算法:%.3f" % result.mean())
嶺回歸算法:-23.890
2.1.3套索回歸算法
套索回歸算法與嶺回歸算法類似���,套索回歸算法也會懲罰回歸系數(shù)��,在套索回歸中會懲罰回歸系數(shù)的絕對值大小����。此外�����,它能夠減少變化程度并提高線性回歸模型的精度����。
from sklearn.linear_model import Lasso
#套索回歸算法
model = Lasso()
scoring = 'neg_mean_squared_error'
result = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("套索回歸算法:%.3f" % result.mean())
套索回歸算法:-28.746
2.1.4彈性網(wǎng)絡回歸算法
彈性網(wǎng)絡回歸算法是套索回歸算法和嶺回歸算法的混合體,在模型訓練時彈性網(wǎng)絡回歸算法綜合使用L1和L2兩種正則化方法�����。當有多個相關的特征時�,彈性網(wǎng)絡回歸算法是很有用的,套索回歸算法會隨機挑選一個���,而彈性網(wǎng)絡回歸算法則會選擇兩個���。它的優(yōu)點是允許彈性網(wǎng)絡回歸繼承循環(huán)狀態(tài)下嶺回歸的一些穩(wěn)定性����。
from sklearn.linear_model import ElasticNet
#彈性網(wǎng)絡回歸算法
model = ElasticNet()
scoring = 'neg_mean_squared_error'
result = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("彈性網(wǎng)絡回歸算法:%.3f" % result.mean())
彈性網(wǎng)絡回歸算法:-27.908
2.2非線性算法審查
2.2.1K近鄰算法
在scikit-learn中對回歸算法的K近鄰算法的實現(xiàn)類是KNeighborsRegressor�。默認距離參數(shù)為閔氏距離。
from sklearn.neighbors import KNeighborsRegressor
#K近鄰算法
model = KNeighborsRegressor()
scoring = 'neg_mean_squared_error'
result = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("K近鄰算法:%.3f" % result.mean())
K近鄰算法:-38.852
2.2.2分類與回歸樹
在scikit-learn中分類與回歸樹的實現(xiàn)類是DecisionTreeRegressor�。
from sklearn.tree import DecisionTreeRegressor
#分類與回歸樹算法
model = DecisionTreeRegressor()
scoring = 'neg_mean_squared_error'
result = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("分類與回歸樹算法:%.3f" % result.mean())
K近鄰算法:-38.852
分類與回歸樹算法:-21.527
2.2.3支持向量機
from sklearn.svm import SVR
#支持向量機
model = SVR()
scoring = 'neg_mean_squared_error'
result = cross_val_score(model, X, Y, cv=kfold, scoring=scoring)
print("支持向量機:%.3f" % result.mean())
支持向量機:-67.641
3.算法比較
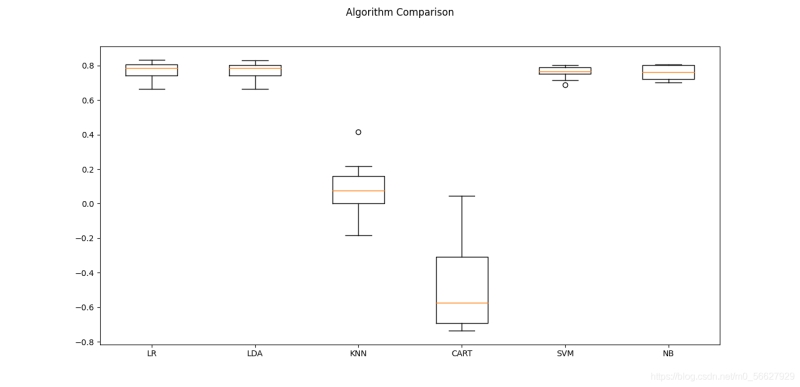
比較不同算法的準確度,選擇合適的算法�,在處理機器學習的問題時是分廠重要的。接下來將介紹一種模式�,在scikit-learn中可以利用它比較不同的算法,并選擇合適的算法�����。
當?shù)玫揭粋€新的數(shù)據(jù)集時��,應該通過不同的維度來審查數(shù)據(jù)���,以便找到數(shù)據(jù)的特征�。一種比較好的方法是通過可視化的方式來展示平均準確度���、方差等屬性�����,以便于更方便地選擇算法��。
最合適的算法比較方法是:使用相同數(shù)據(jù)�、相同方法來評估不同算法�����,以便得到一個準確的結(jié)果����。
使用Pima Indias數(shù)據(jù)集來介紹如何比較算法。采用10折交叉驗證來分離數(shù)據(jù)��,并采用相同的隨機數(shù)分配方式來確保所有算法都使用相同的數(shù)據(jù)����。為了便于理解,為每個算法設定一個短名字�。
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from matplotlib import pyplot
filename = 'pima_data.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(filename,names=names)
array = data.values
X = array[:,0:8]
Y = array[:,8]
num_folds = 10
seed = 7
kfold = KFold(n_splits=num_folds,random_state=seed,shuffle=True)
models={}
models['LR'] = LogisticRegression(max_iter=3000)
models['LDA'] = LinearDiscriminantAnalysis()
models['KNN'] = KNeighborsRegressor()
models['CART'] = DecisionTreeRegressor()
models['SVM'] = SVC()
models['NB'] = GaussianNB()
results = []
for name in models:
result = cross_val_score(models[name], X, Y, cv=kfold)
results.append(result)
msg = '%s: %.3f (%.3f)' % (name, result.mean(), result.std())
print(msg)
#圖表顯示
fig = pyplot.figure()
fig.suptitle('Algorithm Comparison')
ax = fig.add_subplot(111)
pyplot.boxplot(results)
ax.set_xticklabels(models.keys())
pyplot.show()
執(zhí)行結(jié)果如下:
LR: 0.772 (0.050)
LDA: 0.767 (0.048)
KNN: 0.081 (0.159)
CART: -0.478 (0.257)
SVM: 0.760 (0.035)
NB: 0.759 (0.039)
總結(jié)
本文主要介紹了算法審查以及如何選擇最合適的算法,在第三部分中提供了代碼實例�����,可以直接將其作為模板使用到項目中以選擇最優(yōu)算法。
到此這篇關于Python機器學習入門(五)算法審查的文章就介紹到這了,更多相關Python機器學習內(nèi)容請搜索腳本之家以前的文章或繼續(xù)瀏覽下面的相關文章希望大家以后多多支持腳本之家�!
您可能感興趣的文章:- Python機器學習入門(一)序章
- Python機器學習入門(二)之Python數(shù)據(jù)理解
- Python機器學習入門(三)之Python數(shù)據(jù)準備
- Python機器學習入門(四)之Python選擇模型
- Python機器學習入門(六)之Python優(yōu)化模型
- python機器學習高數(shù)篇之函數(shù)極限與導數(shù)